SVG轻松实现路径动画
前言
最近在学习SVG相关的内容,感叹SVG真的是太强大了。内容之多,根本不是一两篇文章能够涵盖的。所以决定还是找几个小点慢慢学习吧。
很多电商网站里,在加入购物车时都会有一个形象的动画,让宝贝以类似抛物线的轨迹飞进购物车,就像不要钱一样😂 。 像这样:
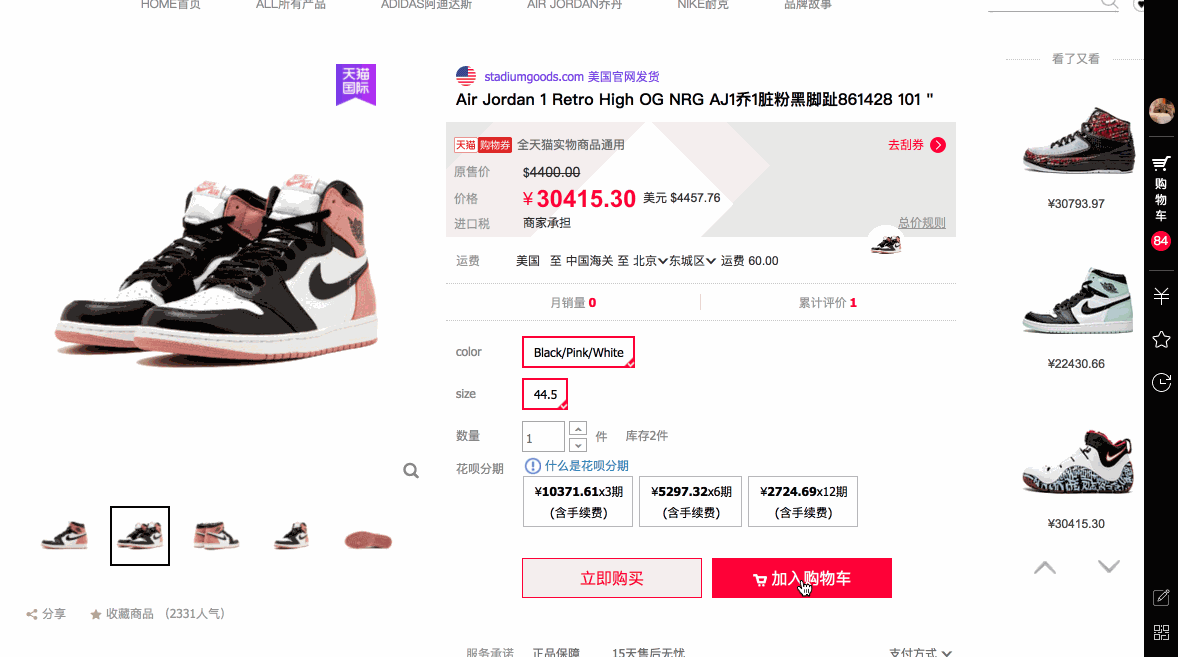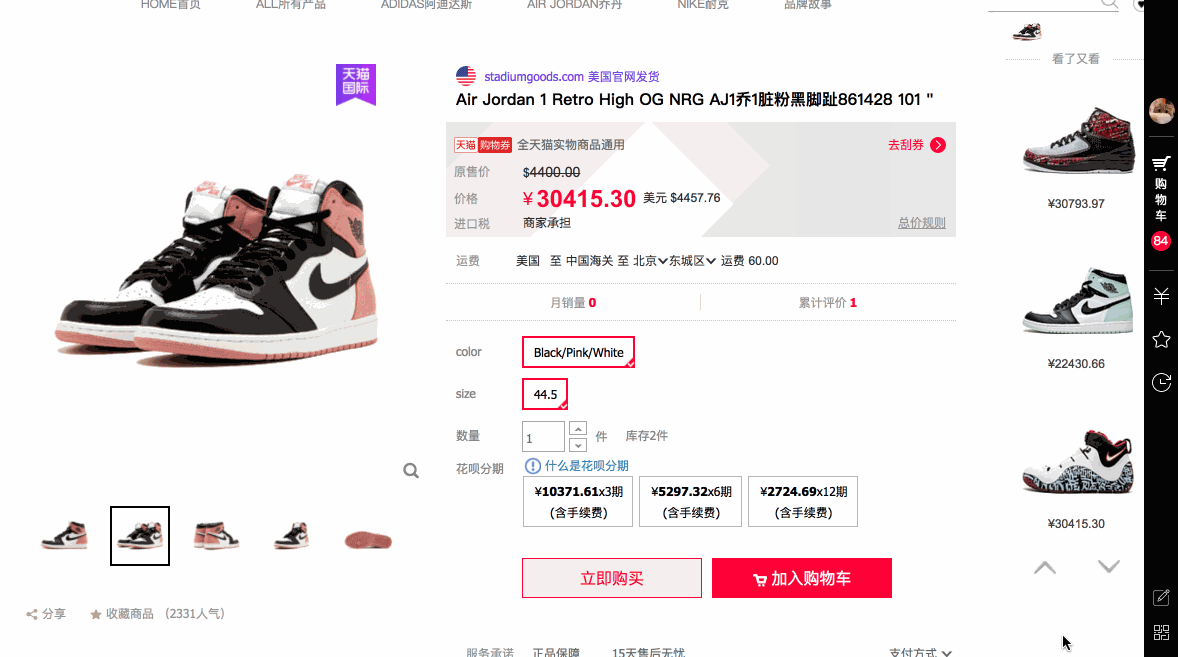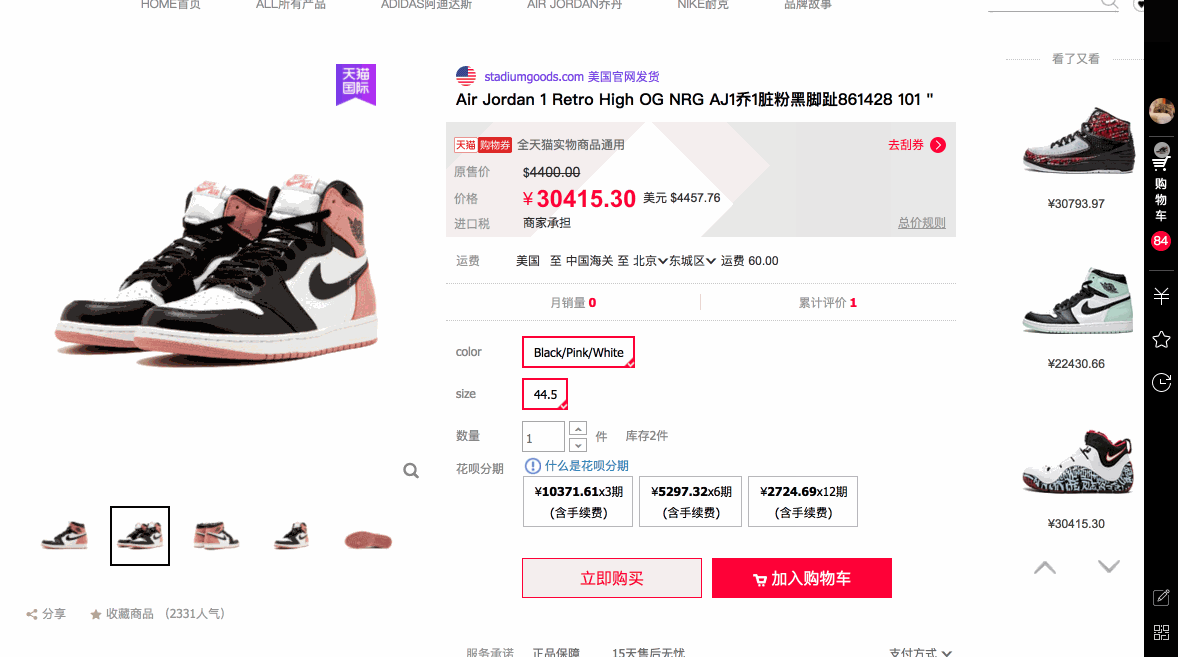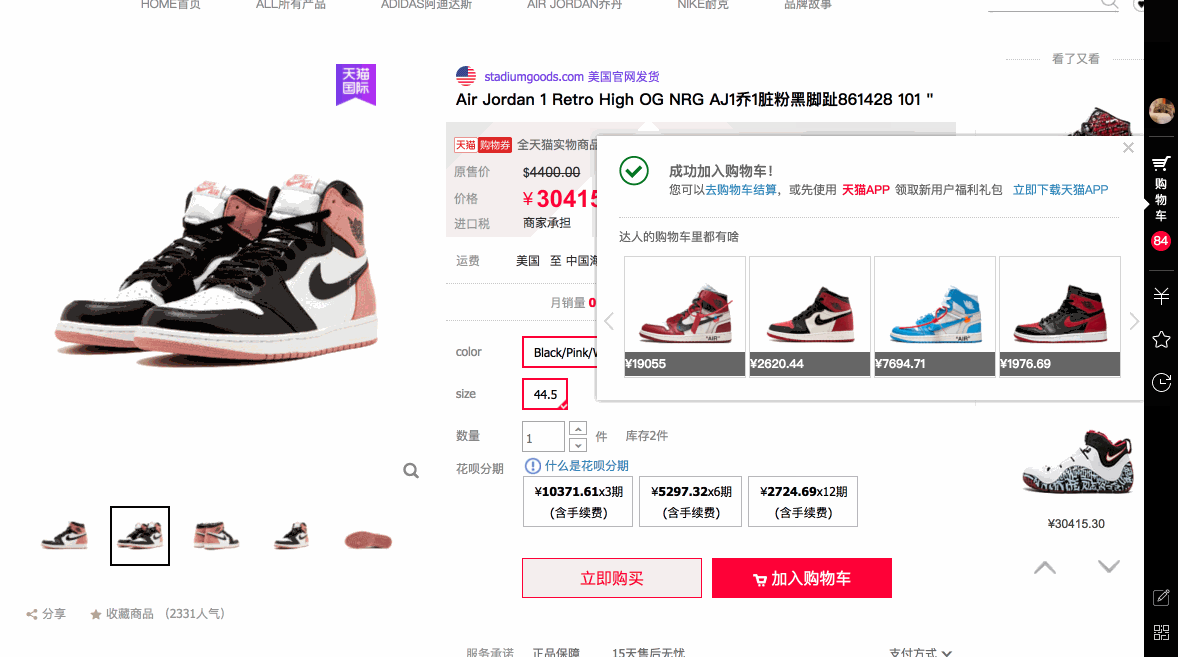
实现这种效果可能有很多方法,但是用SVG可以快速简单的实现。今天我们一块学习一下这个方法。
SVG路径
SVG中最强大的元素莫过于path了,它可以描绘机会任意的2D图形。
一个简单的路径是这样婶儿的:
<path d="M10 10 L75 10 L75 75 Z" />
还有稍微复杂的路径:
<path d="M199.428,125.107C159.17,32.871,44.736,54.392,43.983,161.445c-0.417,58.8,54.491,80.773,91.049,104.277,35.45,22.8,60.68,53.978,64.634,67.252,3.385-13.006,31.486-45.071,64.3-67.889,35.88-24.951,91.466-45.485,91.049-104.279C354.26,53.487,237.835,36.55,199.428,125.107Z"/>
这是一个心形,下面会用到这个路径。当然这种路径不是手动写出来的,而是用专门的软件导出的。这个就是我用PS导出来的。
path有以下这些指令:
| 指令 | 参数 | 描述 |
|---|---|---|
| M(Move to) | x y | 起始点坐标x y |
| L(Line to) | x y | 从当前点的坐标画直线到指定点的 x y坐标 |
| H(Horizontal line to) | x | 从当前点的坐标画水平直线到指定的x轴坐标 |
| V(Vertical line to) | y | 从当前点的座标画垂直直线到指定的y轴坐标 |
| C(Curve) | x1 y1 x2 y2 x y | 从当前点的坐标画条贝塞风线到指定点的x, y坐标,其中 x1 y1及x2, y2为控制点 |
| S(Smooth curve) | x2 y2 x y | 从当前点的坐标画条反射的贝塞曲线到指定点的x, y坐标,其中x2, y2为反射的控制点 |
| Q(Quadratic Bézier curve) | x1 y1 x y | 从当前点的坐标画条反射二次贝塞曲线到指定点的x, y坐标,其中x1 y1为控制点 |
| T(Smooth Quadratic Bézier curve) | x y | 从当前点的坐标画条反射二次贝塞曲线到指定点的x, y坐标,以前一个坐标为反射控制点 |
| A(Arc) | rx ry x-axis-rotation large-arc-flag sweep-flag x y | 从当前点的坐标画个椭圆形到指定点的x, y坐标,其中rx, ry为椭圆形的x轴及y轴的半径,x-axis-rotation是弧线与x轴的旋转角度,large-arc-flag则设定1最大角度的弧线或是0最小角度的弧线,sweep-flag设定方向为1顺时针方向或0逆时针方向 |
| Z(Closepath) | 无 | 关闭路径,将当前点坐标与第一个点的坐标连接起来 |
offset-path、offset-distance
两个都是CSS属性。
offset-path表示元素的运动路径;
offset-distance定义了元素在路径上运动的距离,单位是数值或百分比。
可想而知,用这两个属性就能实现路径动画了,只需改变offset-distance的值即可。
举一个栗子:
demo 🌰
如果是心形的呢,我们让它40s之内转10圈,再来一个栗子:
demo 🌰🌰
贝塞尔曲线
那怎么模拟出抛物线的形状呢?这里想到了贝塞尔曲线,因为path可以很轻松的绘制贝塞尔曲线。 对于贝塞尔曲线其实我不是太了解,只是看着这种曲线就觉得很“性感”,而且貌似阶数越高越是性感😊。
如下面俩图:
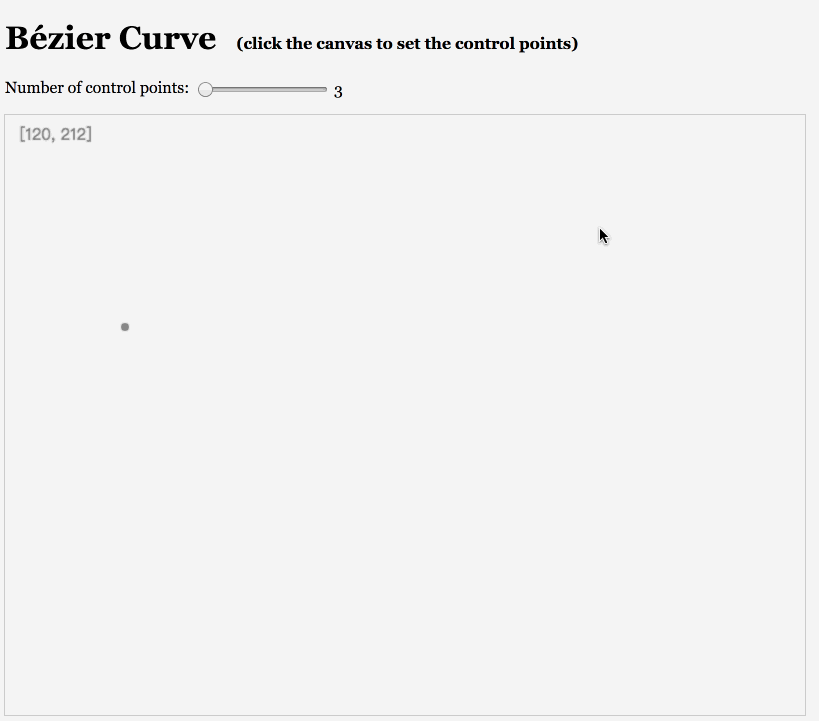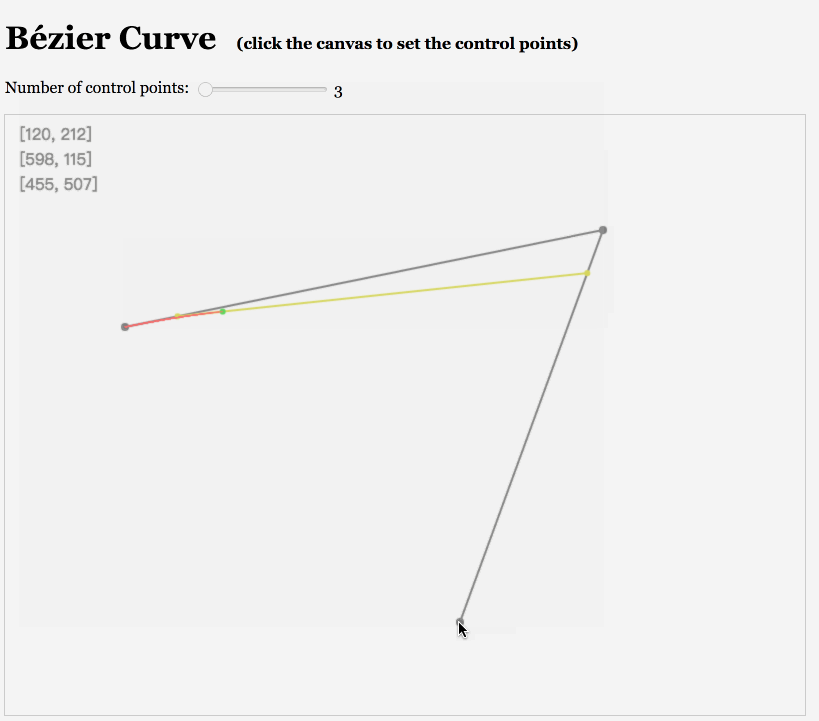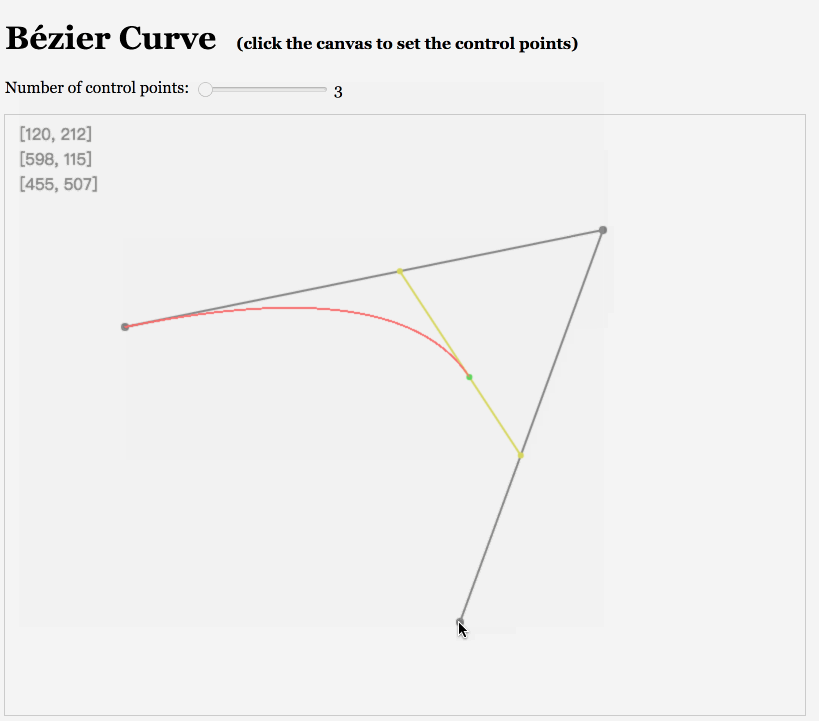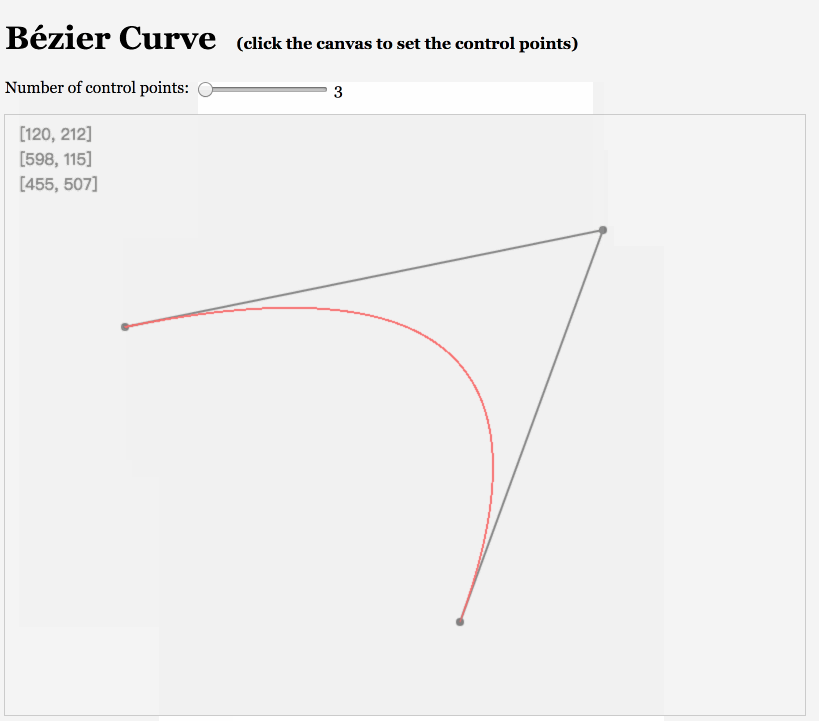
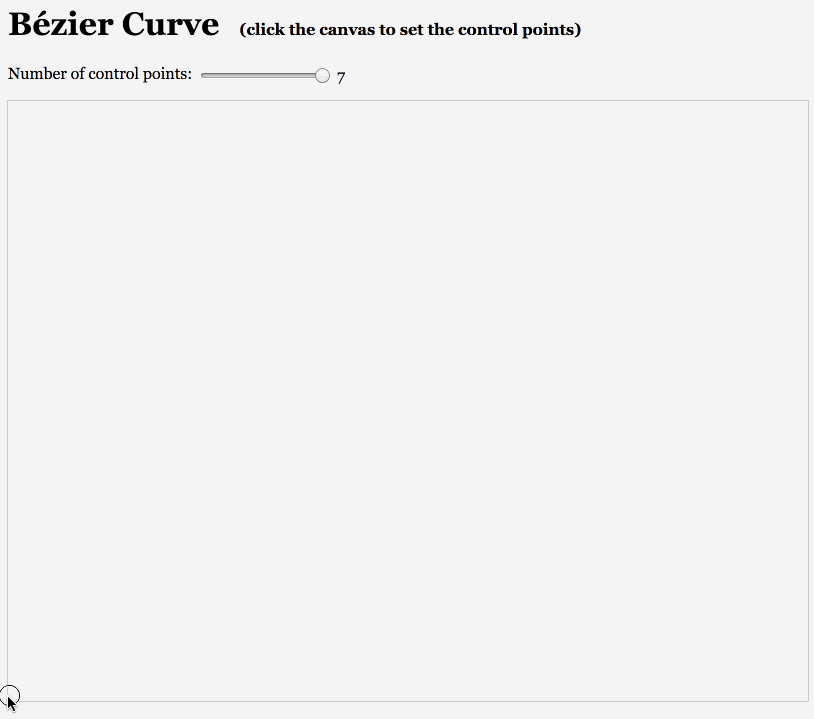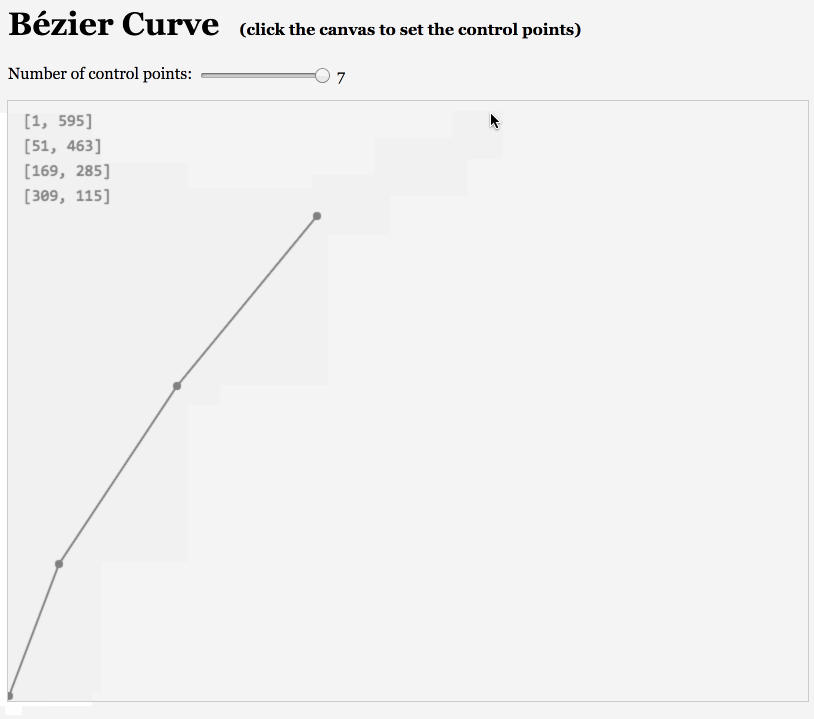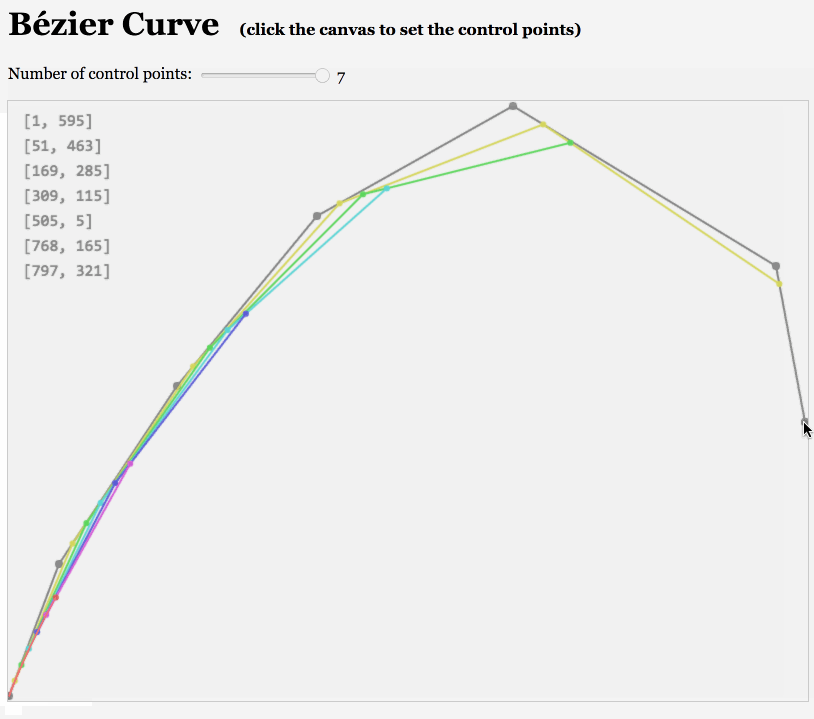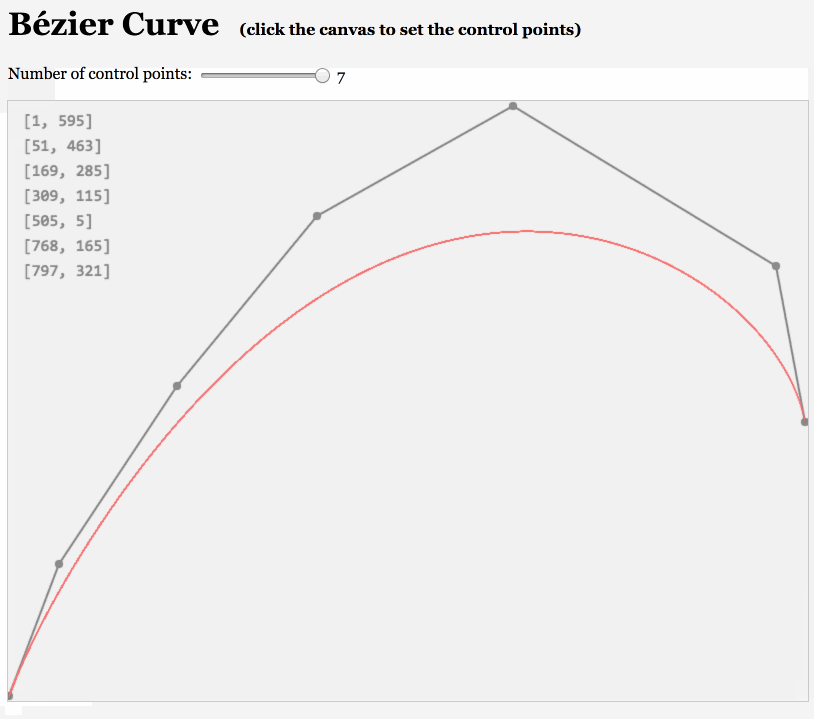
同学们可以自行感受下,
于是我们可以用一个二阶贝塞尔曲线来模拟抛物线的轨迹:我们暂定三个点分别在左下角、上中间和左中间。
这样:
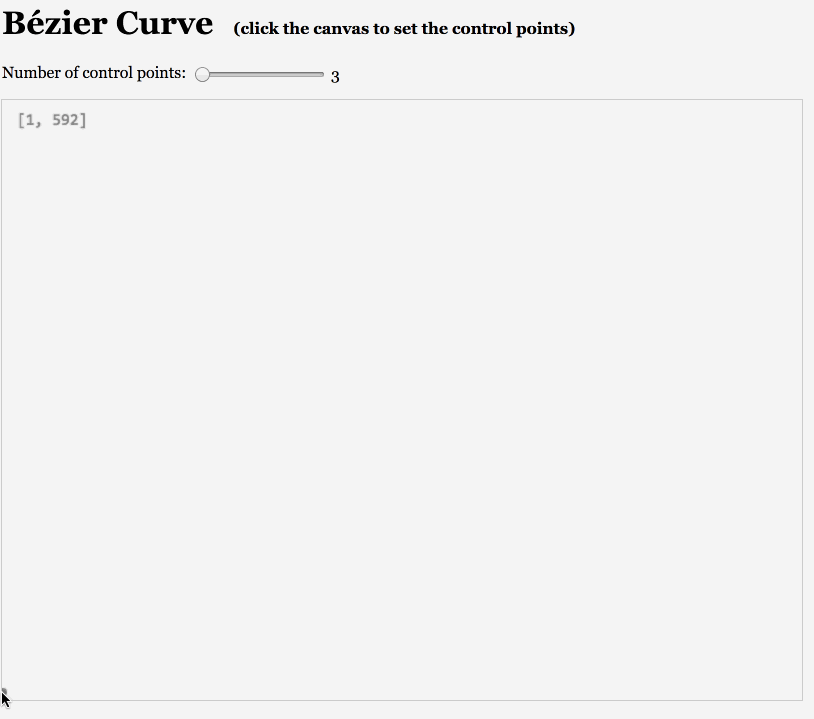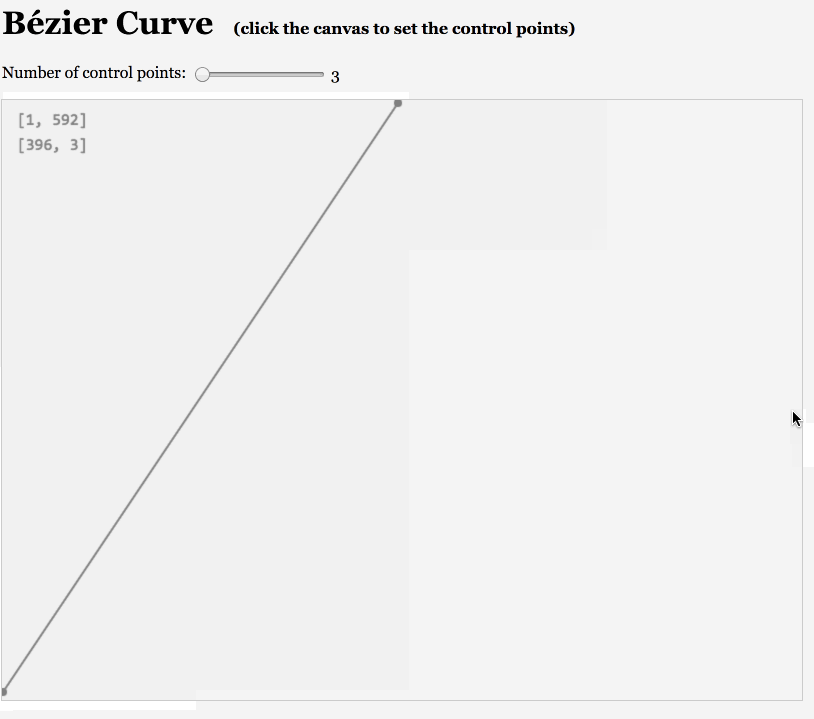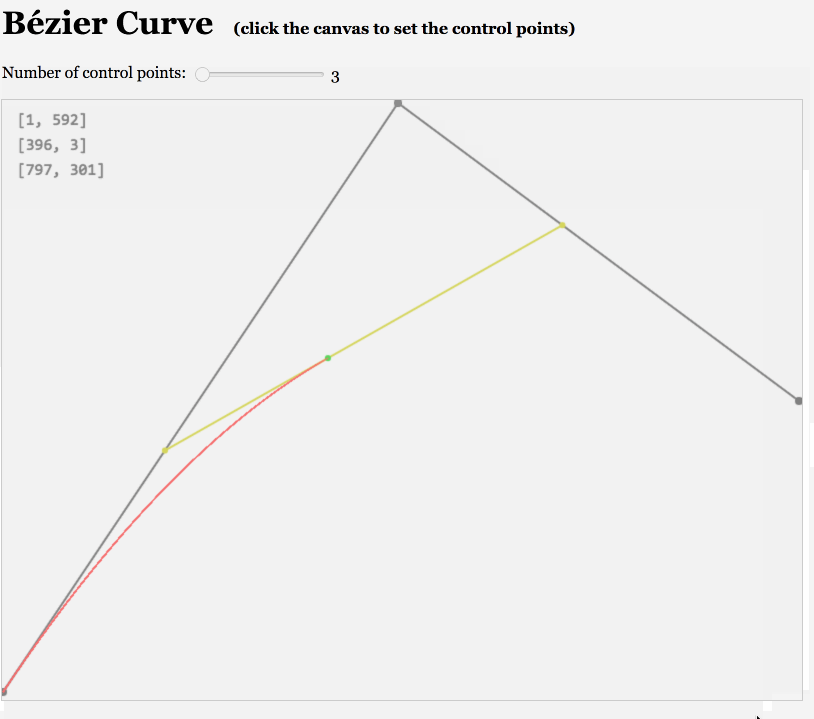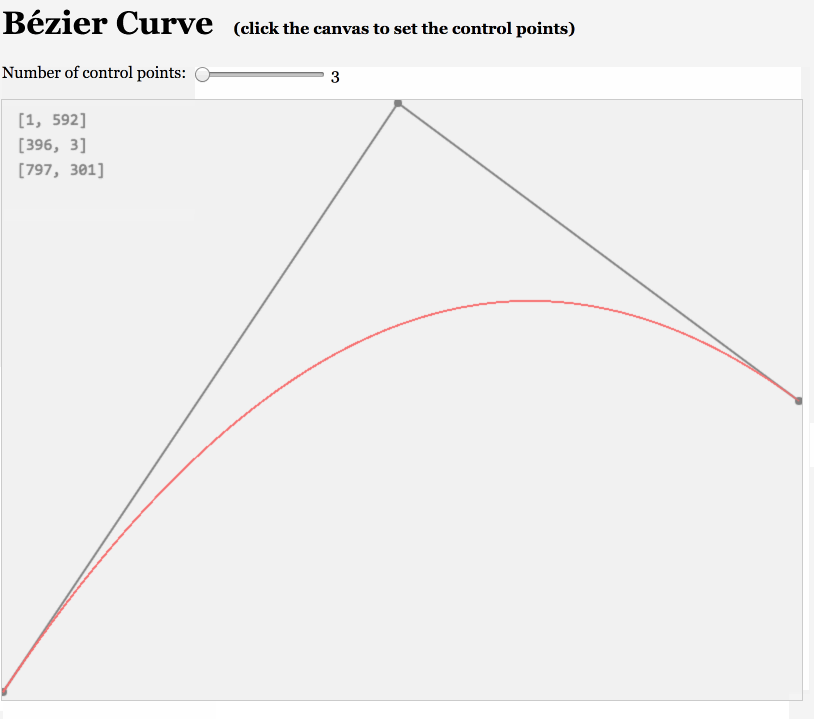
只要在页面上获取到这三个点,就可以了。
又一个栗子:
demo 🌰🌰🌰
继续添加上按钮,加点图片,就是这样的:
demo 🌰🌰🌰🌰
总结
遗憾的是,目前只有Chrome和部分移动端浏览器(如安卓版UC和三星)支持offset-path属性😰。
除此之外,还有三个相关属性:offset-ancor、offset-rotate和offset-position 分别表示锚定的中心点、运动的角度和路径的初始位置,感兴趣的同学可自行前往学习。
